Dynamics
|
|
Generational Dynamics |
| Forecasting America's Destiny ... and the World's | |
| HOME WEB LOG COUNTRY WIKI COMMENT FORUM DOWNLOADS ABOUT | |
|
These pages contain the complete rough draft manuscript of the new book
Generational Dynamics for Historians,
written by John J. Xenakis.
This text is fully copyrighted. You may copy or print out this
material for your own use, but not for distribution to others.
Comments are invited. Send them to mailto:comments@generationaldynamics.com. |
For at least a century, historians have tried to discern war cycles, without much success. Those efforts really took off in the 1920s, right after World War I. However, all those attempts proved to be failures when World War II started.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The most well-known of these efforts is the Kondratiev cycles (K-cycles) theory, developed in the 1920s by Russian researcher Nikolai Kondratiev. He established a war cycle of approximately 50 years. However, his theory was discredited two decades later, since it didn't predict WW II, and in fact was contradicted by WW II.
Supporters of K-cycles and other models tried to repair the theory by saying the World War II was an anomaly, an exception to the rule. But this was a major problem, because WW II should be their best case, according to George Modelski:
[A] large number of other international relations theories were based explicitly on the World War I experience. What would be more desirable is an argument that could handle World Wars I and II simultaneously without resorting to an ad hoc explanation (or simply writing off one of the wars as an exception to the general pattern). The two world wars of the twentieth century are simply too important to dismiss as exceptions, especially if the war / long-term growth linkage is limited to the past two centuries. If one of these wars appears to be an exception to the rule, it may be that either the rule is being misinterpreted or that the rule underwent some type of change during the twentieth century.
The following graph correlating war deaths to K-cycles shows what the problem is. (We've previously seen this graph on page [causes#501]).
 |
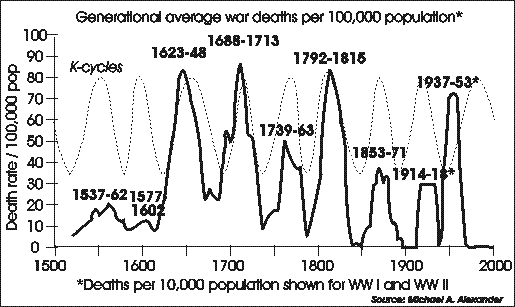The K-cycles are computed from a variety of economic series, the choice depending on the particular researcher. As this graphic shows, war deaths and K-cycles, are pretty well correlated up to World War I, but then completely diverged with WW II.
(We'll use "K-cycles" as a shorthand to refer to a class of related "long wave" theories.)
Different researchers had different theories to explain K-cycles. There are four major explanations, according to Joshua S. Goldstein:
There's a massive period of over-investment of capital goods, which gives way to a period of under-investment and consolidations. Key variables are capital investment and production.These theories were developed during the period between the two world wars, but all of them failed to predict WW II. K-cycles fell out of favor for a while, but interest was revived in the 1980s and 90s.
K-cycles take place in the "Whole World View" (see p. [forecast#805]) of the Generational Dynamics "magic ball of yarn" model.
In this view, wars take place as completely chaotic events, so there should be no pattern at all. In this chapter we won't enter the debate about why there's a pattern, or what generates the pattern. Our purpose here is to acknowledge that they exist, and incorporate them into the Generational Dynamics model.
From the point of view of Generational Dynamics, much of the K-cycles research simply makes no sense whatsoever, especially in the choice of variables. Generational Dynamics provides a great deal of information on how variables should be selected for K-cycles and other long wave theories.
In order to correlate economic variables to war variables, you have to choose which wars you're going to correlate to.
It's very important that wars be chosen according to specific, defensible rules, for otherwise the researcher may be suspected of "cherry-picking" wars to make the correlation come out as desired.
As I read some of the literature on Kondratiev cycles, I find it hard to understand what wars the authors are choosing. What wars should be chosen? Should they be West European wars? That seems to be the case in some literature, but Kondratiev was Russian, and particularly interested in WW I, which was an East European war. In reading the literature, I get the feeling that researchers are selecting wars from specific regions (not often explicitly identified), thus using a rough "Principle of Localization," though not always in a sufficiently precise way.
Obviously the choice of wars should depend on the properties of the economic variable being correlated, but Generational Dynamics tells us that there are some things we can say immediately.
First off, crisis wars and non-crisis wars have to be sorted into separate series. Crisis wars are launched by large masses of people because of deep visceral hatred, while non-crisis wars are limited objective wars launched by politicians for purely political expedience, and ended when it's politically expedient to end it. There is absolutely no à priori reason why anything that correlates to crisis wars should also correlate to non-crisis wars. The burden of proof for intermingling crisis and non-crisis wars is on the researcher, and must be fully justified.
In the case of K-cycles, there's a special irony coming from the fact that Western researchers have been trying to build on a theory developed by a 1920s Russian. World War I was on the East European timeline, and so the fact that K-cycles didn't predict WW II might be perfectly legitimate, since WW II is a West European war.
In fact, it's important to remember that war variables are local variables, local to a particular society, nation or region. If Ireland has a civil war, then there's absolute no à priori reason to believe that it will cause (or prevent) a war in Italy, Africa or China. There is no relationship between regional wars in different areas, unless some phase locking mechanism can be found -- such as a treaty or close identify groups (common religion, skin color, ethnicity, language, etc.).
Technology variables are quite different from war variables, because they're global, rather than local. There is, in fact, a rough phase locking mechanism which causes technological developments to be synchronized between countries. It's the obvious one - that technological developments in one country are soon carried to other countries and adopted there. Over the centuries, new communications and transportations inventions shortened the synchronization times from years and months to weeks and day.
One of the reasons given in the theories we listed above for the existence of K-cycles was cycles in innovation and technology. If this is true, then technology may itself be a kind of phase locking device for wars. Once again, the mechanism may be the obvious one: When a country develops (or otherwise obtains) new technology, it may be more inclined to launch a non-crisis war to take advantage of the new technology.
Once again, great care must be taken to separate out different classes of financial variables:
An illustration of the interaction of technology and financial variables is illustrated by the following chart, which we've already seen in the last chapter, of stock prices since 1871:
 |
This chart shows the S&P 500 index in constant dollars, labeling the 1920s and 1990s generational bubbles.
The smoothing line is almost a perfect fit to the actual S&P curve, provided that you ignore the generational bubbles and their aftermath.
This diagram illustrates the important point that if you want to find patterns in financial cycles, then you have to separate out the generational bubbles, because they're completely unrelated to the rest of the cycle.
We are now going to add K-cycles to the "magic ball of yarn" Generational Dynamics model. In particular, we will be examining the the "Whole World View" (see p. [forecast#805]) of the model.
Although we tend to favor the technology and innovation explanation for the K-cycles, we will not assume that. In fact, we won't assume anything, except that the K-cycles exist. We simply add the K-cycles to the Whole World View of the model, and we show from the model why K-cycles worked in earlier centuries, but failed in the 20th century.
This is a fairly "unnatural" way of doing things. What we'd really like to do is postulate some sort of phase locking by individuals performing innumerable individual chaotic actions, and then prove the existence of a attractor that generates a cyclic pattern that satisfies the properties of the K-cycles.
However, that's more than we need to do. We're simply going to superimpose the K-cycle attractor on top of the "Whole World View" of the model, and show what happens when we do that. The results are quite startling.
The idea is this: When you look at the world as a whole, crisis wars have occurred throughout history, at fairly random times. Therefore, until the last century or two, the K-cycle attractor that we're postulating dominated the crisis wars.
However, timelines have been merging over the centuries, and in recent times, crisis wars have become far less random, and they've been dominating the K-cycle attractor.
We'll start by showing the effect of the postulated K-cycles on the World War II timeline.
Take a look at the graph below, which is simple numeric model for the years 1000-2010. Take a look at the individual lines from the bottom up:
The 11 local regions are set up so that the cycles merge over time, leading to a major "clash of civilizations" world war in the 2000s decade.
What is the graph measuring? It could be any of the commonly measured variables -- battle deaths, financial cycles, unrest events -- anything that might be generational.
The following graph is the result. [Note: The words "Technology effect" appearing in this graph should be replaced by "K-cycle."]
|
Early in the millennium, when all the generational periods are diffused over time, it's the K-cycle that dominates most of the time.
By the end of the millenium, when the generational periods are merging, it's the generational crisis wars that dominate, and produce higher spikes.
The above graph models the World War II timeline. The 11 regions being modeled in that graph are drawn from the war theatres in Western Europe and the Pacific.
|
We now create a second similar graph to represent the World War I, with regions drawn from war theatres in East Europe and the Mideast.
This graph was generated exactly the same as the previous one, except that all the crisis wars in the 11 regions on the bottom are shifted left 20 years (except for 2010 war).
|
Now we move to the final step -- adding the two graphs together. This gives us the adjoining graph.
This final graph fairly accurately represents the interactions of the K-cycles with generational cycles. In early centuries, the K-cycles dominate the peaks; in the last centuries, the generational crisis wars dominate, culminating in the WW I and WW II peaks in the 20th century. The final war, the "clash of civilizations" world war, is shown on the far right.
Incidentally, these graphs don't adjust for increases in population, especially the dramatic reduction in childhood mortality since the late 1800s. If the models are adjusted for this, then the spikes for WW I and WW II and the final clash would be many times higher.
The modeling done in this chapter strengthens the credibility of Kondratiev cycles, because it shows that the K-cycles can be merged with Generational Dynamics modeling and gets a result that reflects the real world.
However, this modeling does not answer the question of where K-cycles come from in the first place. There is a great deal more K-cycles research to be done. What this chapter makes clear is that crisis and non-crisis wars must be separated and treated as separate data series.
Generational Dynamics provides an explanation of the causes of crisis wars, but provides no clue regarding the causes and frequencies of non-crisis wars. It's possible that further work and research on K-cycles will answer that question. If so, then the result will be a complete answer to the question: Why do we have wars?
